この用語のポイント
簡単にいうと…
ボイル＝シャルルの法則とは
①気体の圧力が一定のとき、温度と体積が比例する（シャルルの法則）
②気体の体積が一定のとき、圧力と温度が比例する（ゲイ＝リュサックの法則）
③気体の温度が一定のとき、体積と圧力が反比例する（ボイルの法則）
という３つの自然法則の総合です。
$\frac{ 圧力 \times 体積 }{ 絶対温度 }$ = 一定と書きます。
詳しくいうと…
シリンダーとはお鍋、ピストンとはその蓋のことです。
（ただしお鍋の蓋は上下に可動するものとする）
このシリンダー（お鍋）の中には、何かの「気体」が詰まっています。
気体は、周囲へ拡散しようと、圧す力（圧力）を外側へ生じさせていて、
上図では、ピストン（お鍋の蓋）の上から押す力と拮抗しているものとします。
①気体の圧力が一定のとき、温度と体積が比例
ここで、シリンダー（お鍋）に火をかけてみましょう：
気体の圧力が一定になるように火をかけると、
シリンダー内部の気体は、その「温度」を上げます。
その結果、シリンダー内部の空間でもある気体の『体積』が上に広がります。
さて、ボイル＝シャルルの法則とは次のとおりです：
$\frac{ 圧力 \times 体積 }{ 絶対温度 }$ = 一定
たとえば、変化前の気体が温度40℃かつ体積1000cm$^3$、
変化後は温度80℃であったとして、
圧力は一定になるよう火をかけているのでどちらもpと置いて、
火にかける前： $\frac{ p \times 1000cm^3 }{ 40℃ }$ = 一定
火にかけた後： $\frac{ p \times ？cm^3 }{ 80℃ }$ = 一定
。。。と書きたくなりますが、シャルル＝ボイルの法則では
温度は摂氏（℃）ではなく、「絶対温度（K）」を使い、
摂氏の値に273を足して絶対温度を表現するため、次のようになります：
火にかける前： $\frac{ p \times 1000cm^3 }{ 40+273 }$ = 一定
火にかけた後： $\frac{ p \times ？cm^3 }{ 80+273 }$ = 一定
両者をひとつにすると…
$\frac{ p \times 1000cm^3 }{ 313K } ＝ \frac{ p \times ？cm^3 }{ 353K } $= 一定
$？cm^3 ＝ \frac{ 1000cm^3 \times 353K }{313K}$
$？cm^3 ＝ 1127cm^3$
となり、気体の温度を40℃→80℃にすると、体積がだいたい1.12倍ちょっと広がることがわかります。
②気体の体積が一定のとき、圧力と温度が比例
つぎに、シリンダー（お鍋）に火はかけたまま、
ピストン（蓋）にテープを張って固定させると、どうなるでしょうか：
蓋は動かないわけですから、体積は一定のままです。
この場合、火にくべることで気体の温度が高まると、
気体の圧力が高まります。
気体の温度が上がることは、気体分子の運動が激しくなることと同じです。
なのでこの状態は、気体分子が熱くなって暴れまわることで
圧力（お鍋の中から脱出しようとする気体の運動）が高まるイメージです。
もう一度ボイル＝シャルルの公式にあてはめて考えてみましょう：
$\frac{ 圧力 \times 体積 }{ 絶対温度 }$ = 一定
今回は、体積が一定です（vとしましょう）。
温度は引き続き40℃→80℃に上がり、
火にかける前の圧力は1.0×105Paとして、火にかけた後の圧力を求めます：
火にかける前： $\frac{ 1.0 \times 10^5 Pa \times v }{ 40+273 }$ = 一定
火にかけた後： $\frac{ ？Pa \times v }{ 80+273 }$ = 一定
$\frac{ 1.0 \times 10^5 Pa \times v }{ 313K } ＝ \frac{ ？Pa \times v }{ 353K }$
$？Pa ＝ \frac{ 1.0 \times 10^5 Pa \times 353K }{ 313K }$
$？Pa ≒ 1.1278 \times 10^5Pa$
となり、やはり約1.12倍ちょっと、気圧の高まったことがわかります。
ちなみに、逆も真で、圧力が上がっても温度は上がります。
たとえば、このお鍋がとても頑丈で形が変わらないとして（体積はつねに一定）、
蓋を閉めたままマリファナ海溝（高圧環境）に沈めてやると、
鍋の外部からかかる高圧に比例して、鍋内部はとても高温になります。
この現象を利用して、エアコンや冷蔵庫の「コンプレッサー（圧縮機）」は
気体状態の冷媒を加圧し、冷媒の温度を高めています。
またそれらの「膨張弁」は、逆に、
冷媒を減圧し、温度を低くさせています。
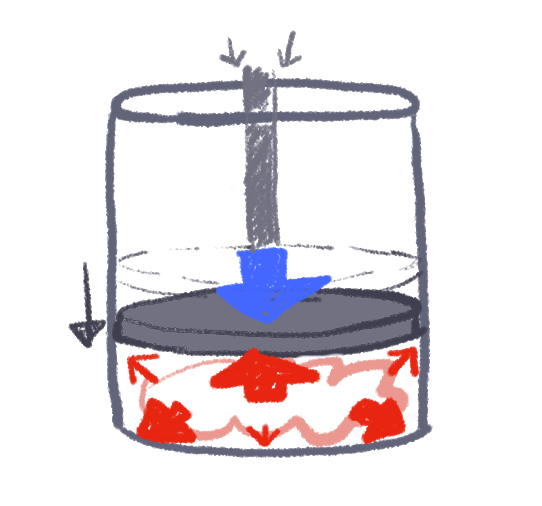
③気体の温度が一定のとき、体積と圧力が反比例
最後に、火はとめてあげて、
ピストン（お鍋の蓋）を押し下げてみましょう：
蓋に力を加えると、あるところで蓋の沈没が止まります。
これは、蓋の上からかかった強く増した圧力と、蓋の下からかかる気体内部の圧力が
拮抗しているためです。
このとき、気体の圧力は依然と比べて増していることがわかります。
温度は一定に、という設定にここではしたいので
この圧縮に伴い生じる熱は、お鍋の外へ逃げてしまったとしましょう（非断熱）。
そして蓋は下がっているわけですから、
もちろんお鍋内部の空間（気体の体積）も小さくなります。
富士山（低圧状態）で飲んだペットボトルを、下山後の地上（高圧状態）でリュックから取り出すとへこんで体積が減っているのはこのためです。
ボイル＝シャルルの法則にあてはめてみましょう：
$\frac{ 圧力 \times 体積 }{ 絶対温度 }$ = 一定
今回、温度は一定でした（kと書きます）。
圧力が1.0×10$^5$Pa→ 2.0×10$^5$Paへと高まり、
火にかける前の体積が100cm$^3$とすると、
$\frac{ 1.0 \times 10^5 Pa \times 100cm^3 }{ k } ＝ \frac{ 2.0 \times 10^5 Pa \times ？cm^3 }{ k } $= 一定
$？cm^3 = \frac{ 1.0 \times 10^5 Pa \times 100cm^3 }{ 2.0 \times 10^5 Pa }$
$？cm^3 ＝ 50 cm^3$
となり、圧力が倍になると、体積は半分になりましたね（反比例）。
以上がボイル＝シャルルの法則です。
ちなみに、この法則は理想気体（気体分子の体積などを無視したモデル）で適用可能ですが、体積などをもつ実在気体でも近似的に有効だそうです。
さらに知りたいなら…
（←画像クリックでAmazonサイトへ）
個々の法則をがっつり学びたいほどではないけれど、ざっと全体像を掴みたい方向けとなります。
つまり…
ボイル＝シャルルの法則とは
気体における圧力・体積・温度の関係を示す
自然法則というです。
シンプルな関係式じゃな！
歴史のツボっぽくいうと…
1662年 アイルランドのボイルがボイルの法則を示す。
1787年 フランスのシャルルがシャルルの法則を発見。
1802年 フランスのゲイ＝リュサックがゲイ＝リュサックの法則（別名：アモントンの法則）を発表。
<参考文献>（2018/08/15 visited）
