熱力学の法則

Contents

この用語のポイント
簡単にいうと…
詳しくいうと…
さらに知りたいなら…
つまり…
歴史のツボっぽくいうと…

この用語のポイント

・熱の移動にかんする基本法則だよ

簡単にいうと…

熱力学の法則とは

　熱の移動にまつわる４つの基本的性質

を表す自然法則です。

詳しくいうと…

ヤカンを火にかけると、コンロの熱が、ヤカン内の水へと移動して、お湯になります。

熱力学の法則は、こうした熱の移動にかんする基本的性質を示し、以下４つによって表されます：

　第零法則「系AとB、BとCの間に熱の移動がないなら、AとCの間でも熱の移動はない」

　第一法則「系に外界から加わった熱と仕事の総和は、系の内部エネルギーの増加分に等しい」

　第二法則「熱は、ごく自然に高温の物体から低温の物体へと移動し、仕事は、ごく自然に熱へと変換される。それぞれの逆の過程（後者の熱→仕事の場合はその全てが変換される過程）がなされるのは、外界から特殊な工夫を施す場合のみ」

　第三法則「絶対零度で完全結晶のエントロピーは全て等しくなる」

どういうことなのか、それぞれみてゆきましょう。

第零法則

　第零法則「系AとB、BとCの間に熱の移動がないなら、AとCの間でも熱の移動はない」

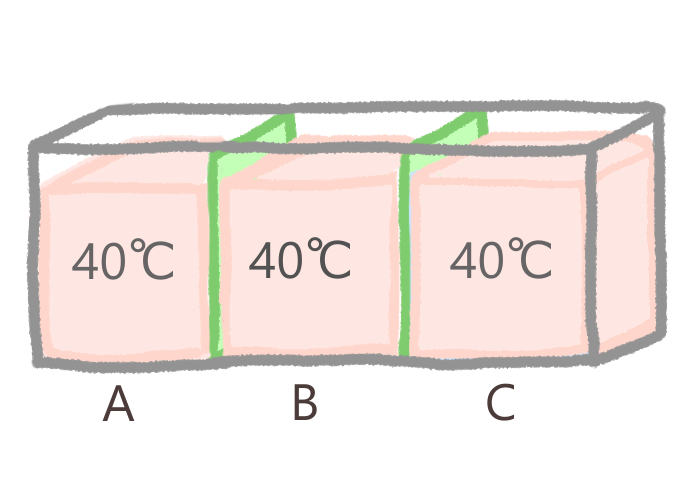
ここに、仕切りで区切られた３つのお湯があります。A、B、Cそれぞれの系の温度は４０℃のようです。

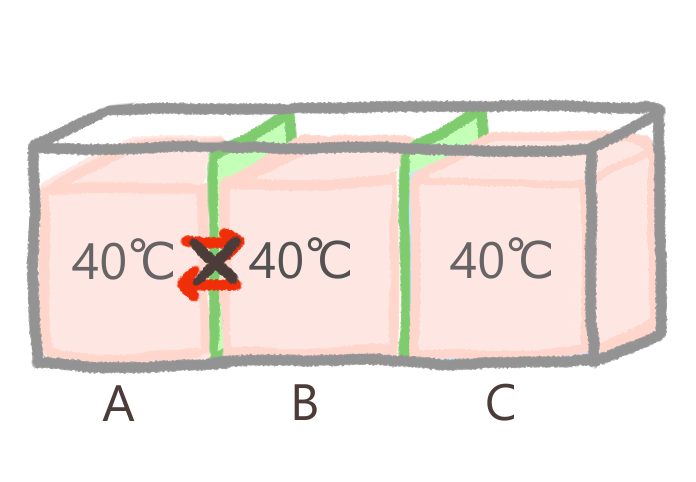
さて、同じ温度（熱量）をもつ系AとBの間では、熱の移動は生じません。

つぎに、系BとCの間でも、同じ温度なので熱の移動は生じません。

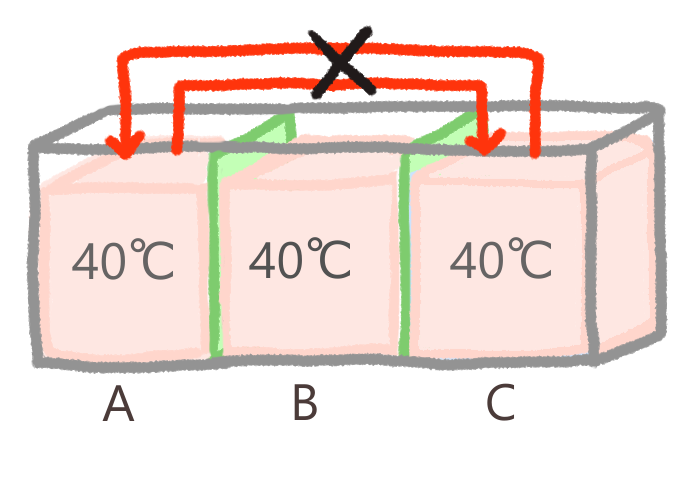
ここから、系AとCの間でも、熱の移動は生じないということが導かれます。

つまり、数学でいう「A＝B、B=Cなら、A=C」みたいなイメージです。

なお、２つの系の間で「熱の移動が生じない」ということは、熱平衡であるともいいます。

ちなみに、この第零法則は温度計による測定の根拠となります。

たとえば、系Bを温度計における水銀だと想像して、”系AとBの熱平衡状態下でこの水銀がある目盛りを示し、系BとCの熱平衡状態下でも前と同じ目盛りを示すなら、系AとCは同じ温度である”、と言える舞台裏では、「系AとCは熱平衡である」と第零法則がお墨付きを与えています。

第一法則

　第一法則「系に外界から加わった熱と仕事の総和は、系の内部エネルギーの増加分に等しい」

ヤカンという系を火にかけたり（熱E）、ピストンを押し込んでシリンダー内容積を圧縮（仕事E）したとします。

すると、ヤカンやシリンダーといった系の内部でうごめいている分子の活動量が、温度の増加という形で活性化します。この分子の活動量を、当の系（物体）の力学的エネルギー（運動E+位置E）に対して、系の内部エネルギーといいます。

右図では、シリンダーに火をかけています。

熱をシリンダーへ移動させた分だけ、シリンダーの内部エネルギーが上昇します。

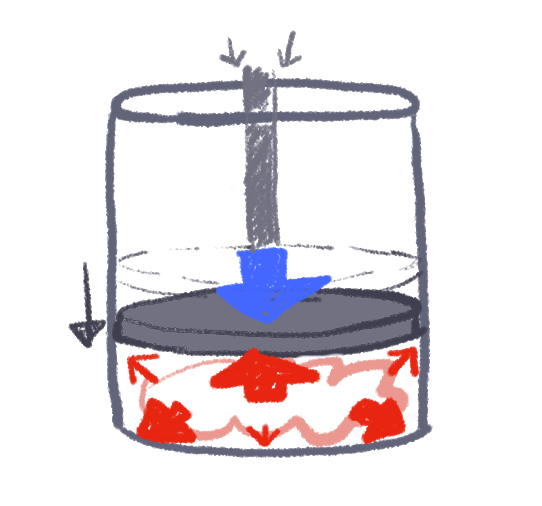
今度は、ピストンを押し込むという仕事Eをシリンダーに対して加えており、その仕事の分だけシリンダーの内部エネルギーはやはり上昇します。

この第一法則のポイントは、熱と仕事（その出入り）が等価に扱われていること。内部エネルギーという考え方を導入することで、熱も仕事も等しく内部エネルギーの上昇／減少に関わるとみなされます。

また、この内部エネルギーの導入によって、ある系に加えられた熱や仕事が、過程のどこかで手品のように消えてしまうことなく、系に蓄えられるのだ、というエネルギー保存則を示してもいます。

この第一法則は、内部エネルギーの増加分が、出入りする熱と仕事の総和であると言っているだけで、内部エネルギーそれ自体の総量については言及していません。

ちなみにここで系とは、閉鎖系（外界と熱と仕事だけを出入りさせる物体）を想定しています。

もし開放系（熱、仕事に加えて、物質の出入りもOKと考えられた物体）を考えるなら、内部エネルギーの上昇／減少には物質も関わることになり、その場合は熱・仕事・物質の総和がその系の内部エネルギーだ、と考えられます。

第二法則

はじめに、高温→低温と、低温→高温にまつわる熱移動の方向性のお話からはじめます。

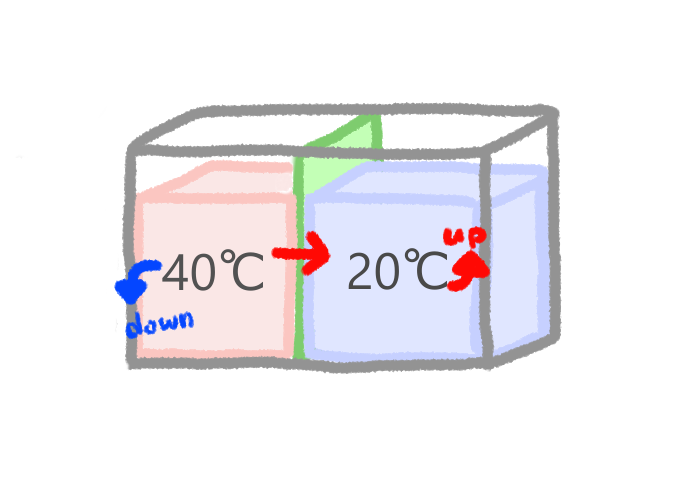
ここに４０℃のお湯の系と、２０℃の水の系が隣接しているとします。

お湯の熱が水のほうへ移動することで、お湯はその温度を下げ、水はその温度を上げます。直感的にも当たり前ですね。

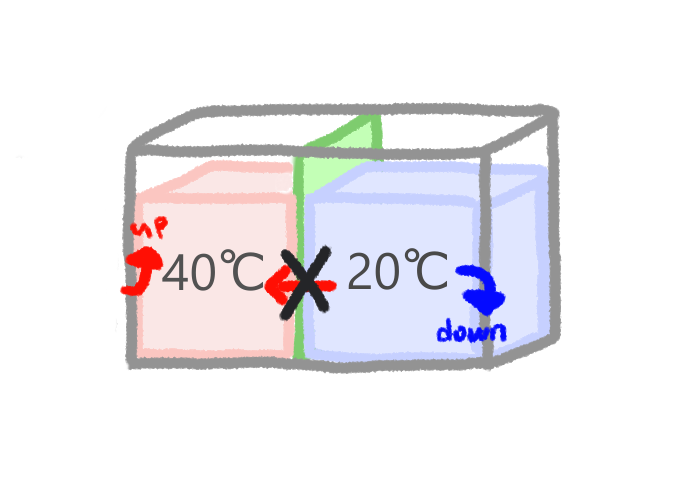
この逆の過程は、いま考えている２つの系のみでは実現不可能です。

水の熱がお湯へと移動することで、水の温度が下がり、お湯の温度が上がることは、ふつうはありえません。

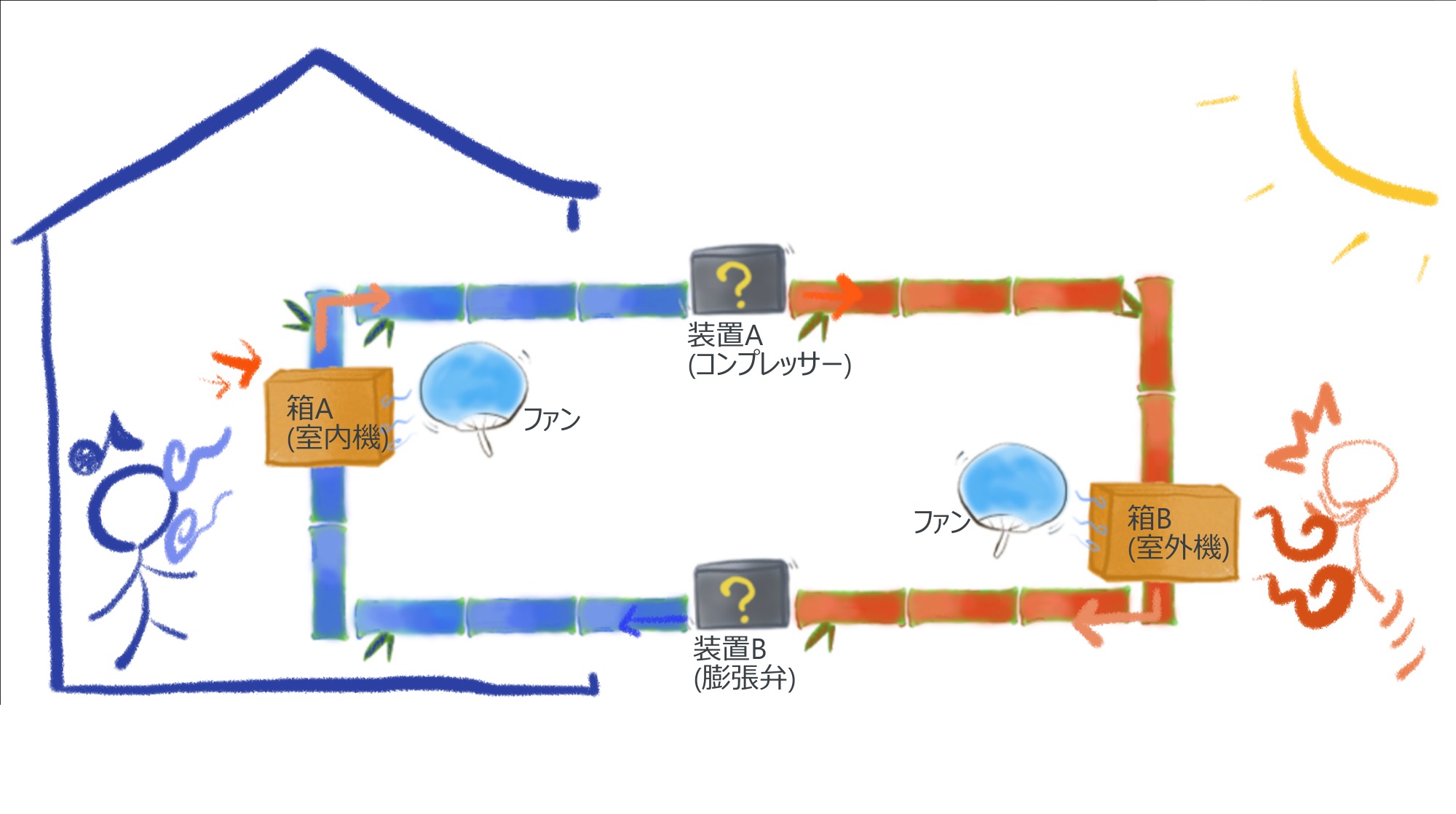
ただし、第三の系を考えるなら話は別です。

右図では、室内という第一の系と、室外という第二の系の間に、エアコンという第三の系を導入しています。

これにより、第一の系（≒水）と第二の系（≒お湯）の間では、低温源から高温源へと熱が移動して、涼しい部屋はより涼しく、熱い街路はより熱くなることがあります。

ただもちろん、エアコンという第三の系なしでは、第一の系と第二の系の間でこのようなことは起こりえません。

以上のことから、熱の移動には、不可逆の方向性のあることがわかります。熱源同士の２つの系しか考えない場合、ごく自然には、高温源→低温源へ、という熱移動の方向性があり、第三の中間系を介入させないかぎり、その逆はありえません。

つづいて、仕事→熱と、熱→仕事にまつわる、エネルギーの質のお話です。

右図では、ピストンを押し込む仕事により、シリンダー内部が高温になっています。仕事→熱への変換の例です。

この場合、ピストンを押し込むために払われた仕事エネルギーの１００％を、理論的にはそのまま熱へ変換することが可能です。

つぎの図では、シリンダーに火をかけ内部の圧力を一時的に増加させることで、体積を膨張させ、ピストンを押し上げて外界へ仕事をしています。先ほどとは逆に、熱→仕事への変換の例です。

この場合、熱エネルギーの１００％を、そのまま仕事へ変換することはできません。

なぜなら、熱がピストンを押し上げるまでの過程で、熱が空気中やシリンダー外壁へと逃げてしまい、仕事にまで結びつかない熱エネルギーがどうしても生じてしまうからです。

この熱放散についていうと、たとえば、わたしたちが料理をしようと、コンロに火をかけて鍋を温めても、火の熱は空気中へと逃げてしまい、台所の気温を上げています。台所の気温を上げることなく鍋のみを温めるのは難しい、ということです。

これは、発電所のボイラーの火でも同じことです。熱のすべてがタービンを回すのに貢献するわけではなく、その熱効率は４０～６０％にすぎません。

以上のことから、エネルギーにはそれぞれ質の程度のあることがわかります。仕事E→熱Eへの変換は容易ですが、熱E→仕事Eへの変換は難しい。このとき、仕事Eは熱Eよりも質が高い、逆に、熱Eは仕事Eより質が低い、と表現します。

このエネルギーの質が一番高いのは原子力Eだといわれています。電気Eも高いです。これらのエネルギーは、自然に任せていると熱Eへと変換されます。そのため、熱Eはあらゆるエネルギーが行きつく墓場とも形容されます。

ちなみに、熱力学にはエントロピーという概念があります。これは、統計力学的にいうと、エネルギーや物質を構成する粒子の分布が各種混合して偏在しているか／偏っているか、粒子分布同士の差異が小さいか（安定しているか）／大きいか（不安定か）に関係するものです。

質の高いエネルギー→質の低いエネルギーへ変換されるに伴って、エネルギーのこのエントロピーも増加してゆきます。
つまり、粒子分布同士の差異が大きく不安定的な（可変的な）エネルギーが、差異の小さな安定的な（不変的な）エネルギーへと変換されます。この変化はごく自然の状態では不可逆的です。
そのため、熱E→仕事Eへと逆方向に変換してエントロピーを減少させるには、人為的に、ある意味で自然の傾向に逆らって非効率なやり方をとらざるをえません。

たとえば、４０℃のお湯の系と２０℃の水の系がある場合、差異の大きい両者を混ぜるとだいたい３０℃の無差異なぬるま湯ができあがりますが（エントロピーの増大）、ここから、ごく自然に、元の４０℃のお湯と２０℃の水が差異化して生じること（エントロピーの減少）はまずありません。

第三法則

　第三法則「絶対零度で完全結晶のエントロピーは全て等しくなる」

温度は、物質内部の分子の熱振動によって表現されるため、まったく分子の振動しない（静止）した下限が考えられます。

絶対零度とは、この温度のとりうる最低値のことで、摂氏だと－273℃、絶対温度だと0K（ケルビン）です。ちなみに絶対零度は、以下で記述するように理屈では考えられますが、実際に実験室内で実現することは不可能な温度とされています（それに近い温度は冷凍ビームなどの技術で可能です）。

完全結晶とは、格子欠陥や不純物のない分子構成の結晶のことです。