この用語のポイント
簡単にいうと…
オットーサイクルとは
ガソリンエンジンという熱機関において、体積・圧力・温度などの関係を、循環プロセスとして定式化した
技術原理です。
ちなみにオットーとは、４ストローク（行程）機関をはじめて実装したといわれる、ドイツの発明家ニコラウス・アウグスト・オットー(1832-1891)にちなんでいます。
詳しくいうと…
ガソリンエンジンのシリンダー内部における
圧力と、体積との関係をグラフにすると、こんな感じになります：
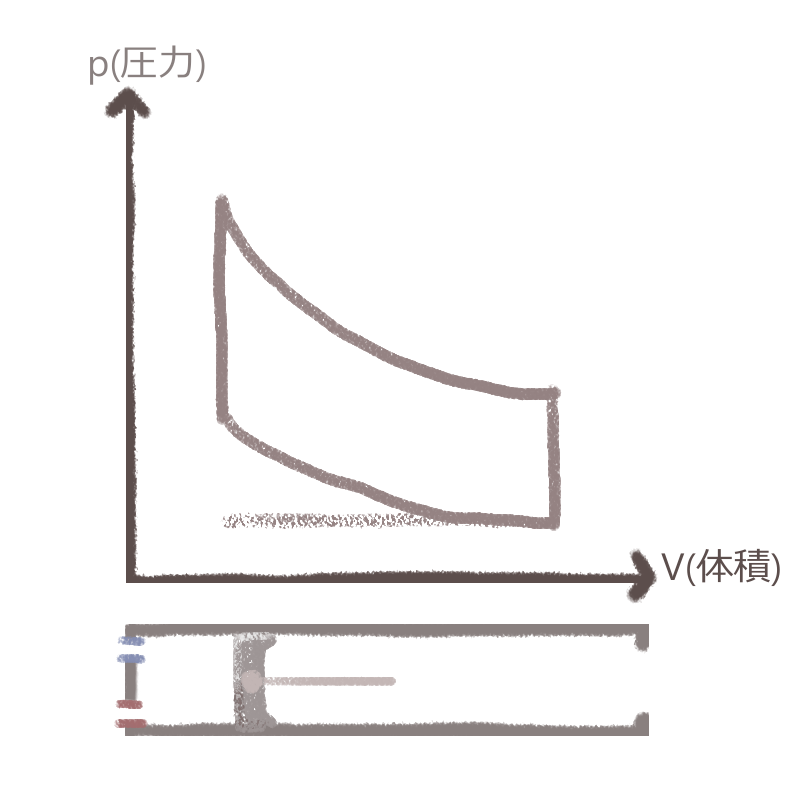左図の下部では、ピストンが上死点（一番奥深く）まで伸びている状態です。
シリンダー内部の体積はこのとき最小になっています。
ここからスタートして、４ストロークの行程それぞれにおける圧力と体積の関係を見てゆきましょう。
まずは吸気の行程からです。
①吸気
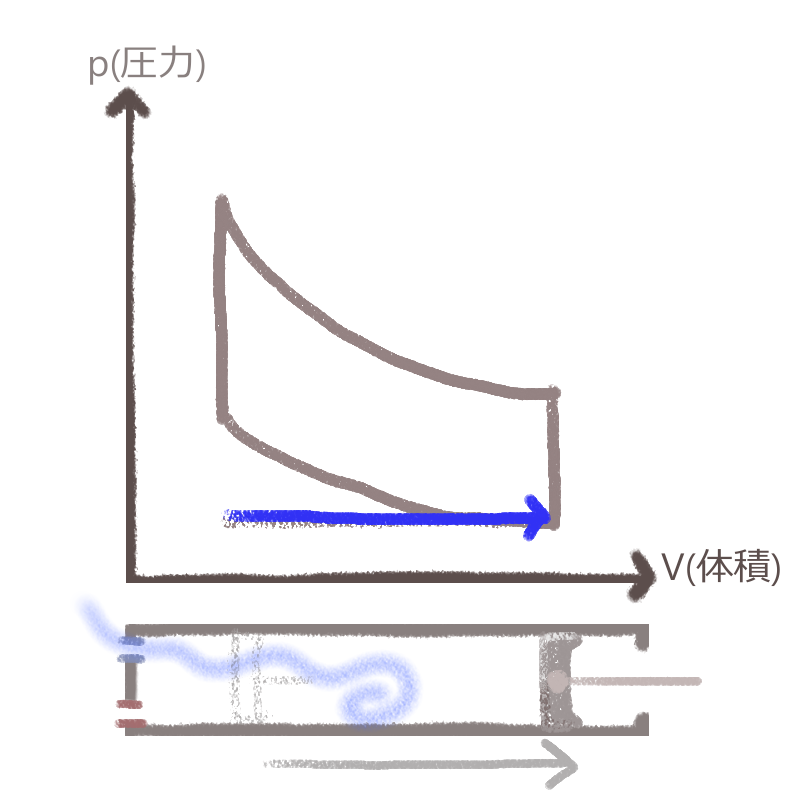
吸気弁から空気を吸い込む際、ピストンは手前に引かれ、シリンダー内部の体積は大きくなります。
グラフ上も、体積が増大する方向へと矢印の移動しているのがわかりますね。
ここではまだ圧力は変化なしなので、横方向のみの移動になります。
②圧縮
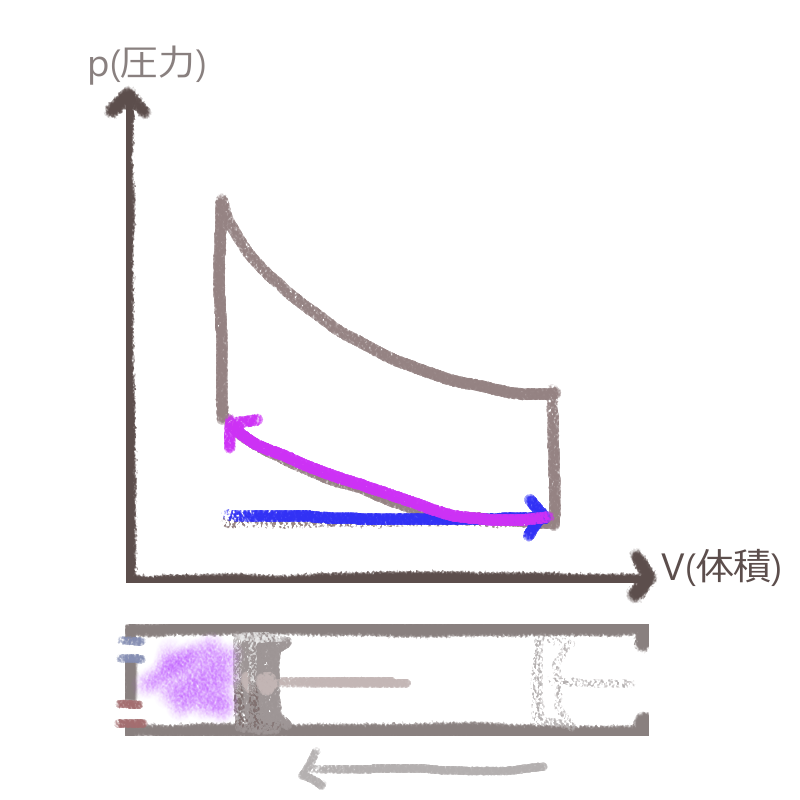
続いて、圧縮の行程です。
ピストンがシリンダーの奥まで詰まってゆき、体積は減少します。
また、このとき吸気弁・排気弁は閉まっている（図では空いてますが、ほんとは閉じてます）ので、逃げ場のない空気の圧力（気体分子がちょこまか動く運動エネルギー）は徐々に高まります。
この結果、グラフ上の矢印は左上方向へ駆け上がりました。
じつは圧縮時に気体の温度も上昇しているのですが、この圧力-体積グラフ上では温度がどうなっているかは見えないようになっています。
③燃焼・膨張
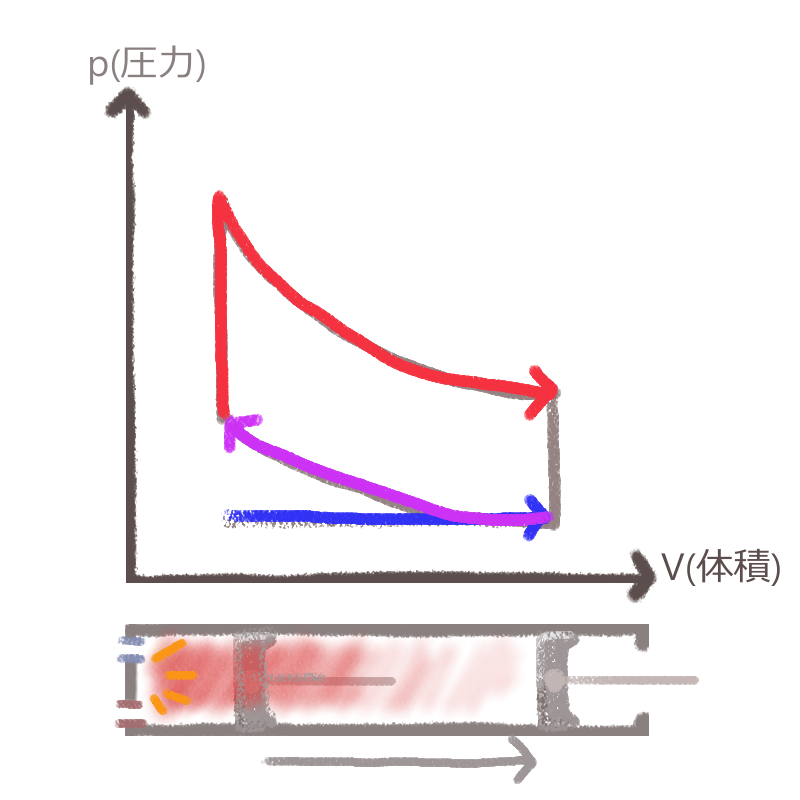
次に、いよいよ燃焼行程です。
点火プラグがスパークし、圧縮気体に着火します。
このとき、ピストンが伸び切った（＝体積が最小）状態のまま、燃焼が一瞬で行われると仮定します。
そのため、グラフ上ではまず、体積は一定のまま、圧力のみが縦方向へ、この燃焼によって急上昇して見えます。
この燃焼＝圧力急上昇を受けて、たまらずピストンは後ろへ押し戻されます。
シリンダー内の体積＝気体の体積は膨張し、また体積が広がった分だけ圧力が低下するので、矢印は右下のほうへと落ちてゆきました。
温度が一定の場合に体積と圧力が反比例する（一方が高まると他方が低くなる）、
という気体の性質については下記用語の記事も参照ください：
④排気
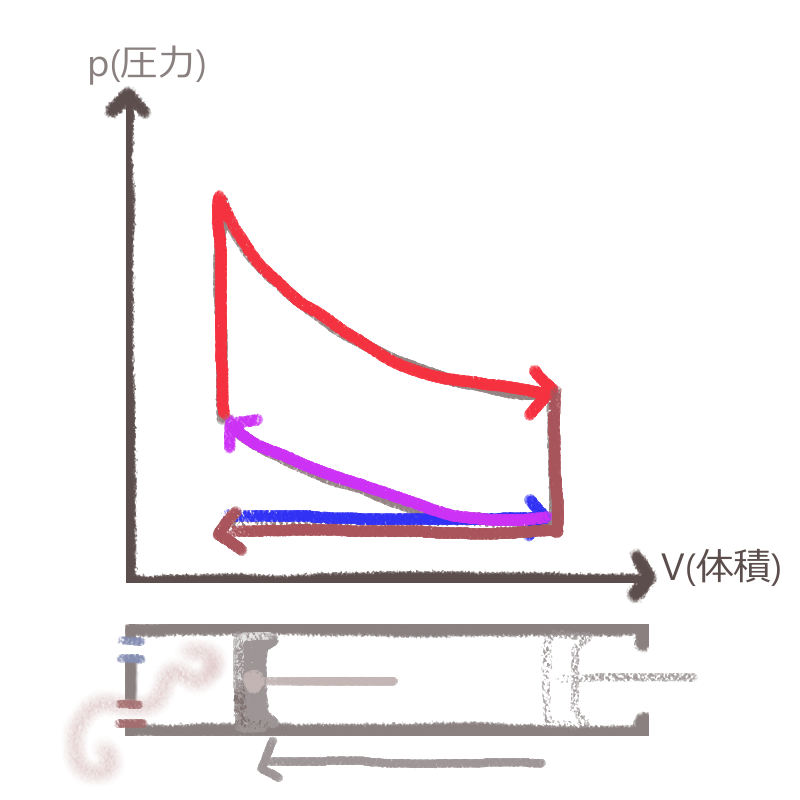
最後に排気行程です。
排気弁が開いたタイミングで、ちょうどピストンがシリンダー奥まで進み、燃焼後の気体を逃がしてやります（排気される気体なので、排気ガスです）。
グラフ上では、いったん排気弁が開いてシリンダー内の圧力が気体とともに逃げてゆくため、真下方向に下がります。
次に、ピストンが押されてシリンダー内の体積が減少するため、矢印は、今度は左方向へと続きます。
以上で、ガソリンエンジン＝４ストローク機関の１サイクルはおしまいです。
この１サイクルの描く閉じた軌跡が、オットーサイクルと呼ばれる循環です。
以降は、このオットーサイクル上の排気行程のゴール地点が、次のサイクルでの吸気行程のスタート地点になり、これら４つの行程が延々とかつ超高速で遂行されてゆきます。
得られた熱と仕事
グラフ上の圧力-体積の関係をひとめぐりしたところで、今度は分析編です。
この１サイクルで得られた仕事、つまり外部にもたらした運動エネルギーを見てゆきます。
この場合の外部とは、車のタイヤであり、そこに至るクランクシャフトであり、そこに至るピストンです。
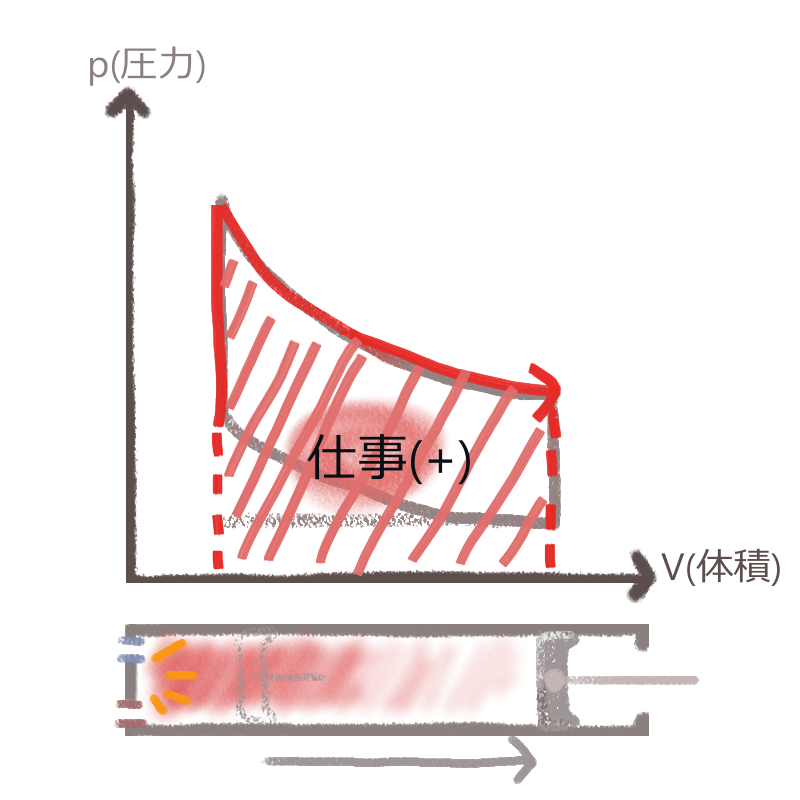
ピストンに運動を与えた行程は、③燃焼・膨張のタイミングでした。
ピストンを押し戻すこの運動は、（押し戻された）体積 ×（膨張時に要された）圧力で求められ、左図のグラフ上の赤い面積部分がその総仕事量にあたります。
ただし、この１サイクル内での仕事の出入りはこの膨張時(out)だけではありません。
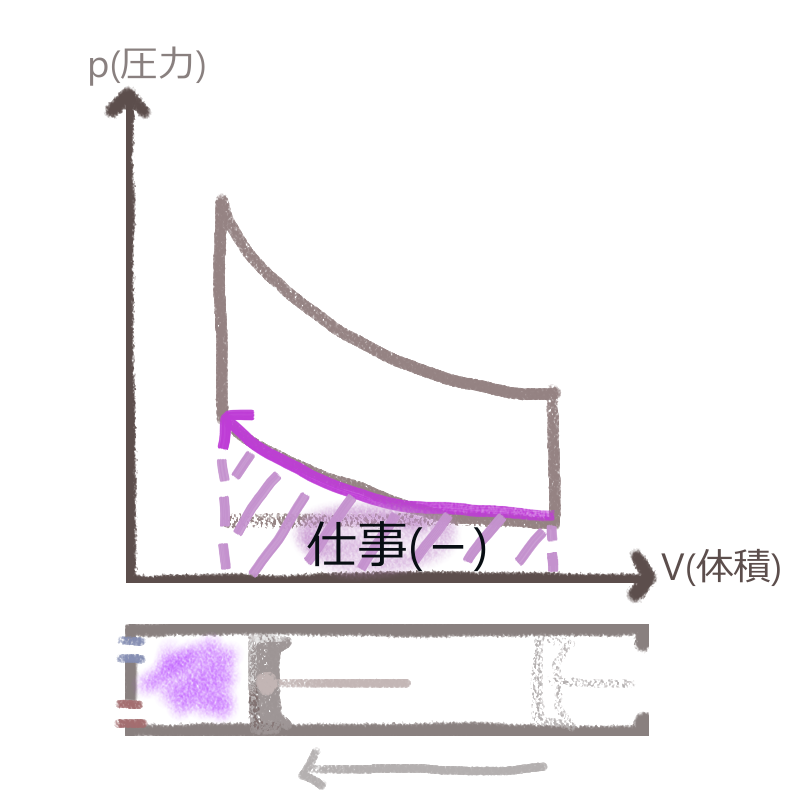
②圧縮時にも、今度はピストンを奥まで押し込むために要された運動エネルギーがありました。
この要された仕事は、左図グラフ上では紫色の面積部分にあたります。
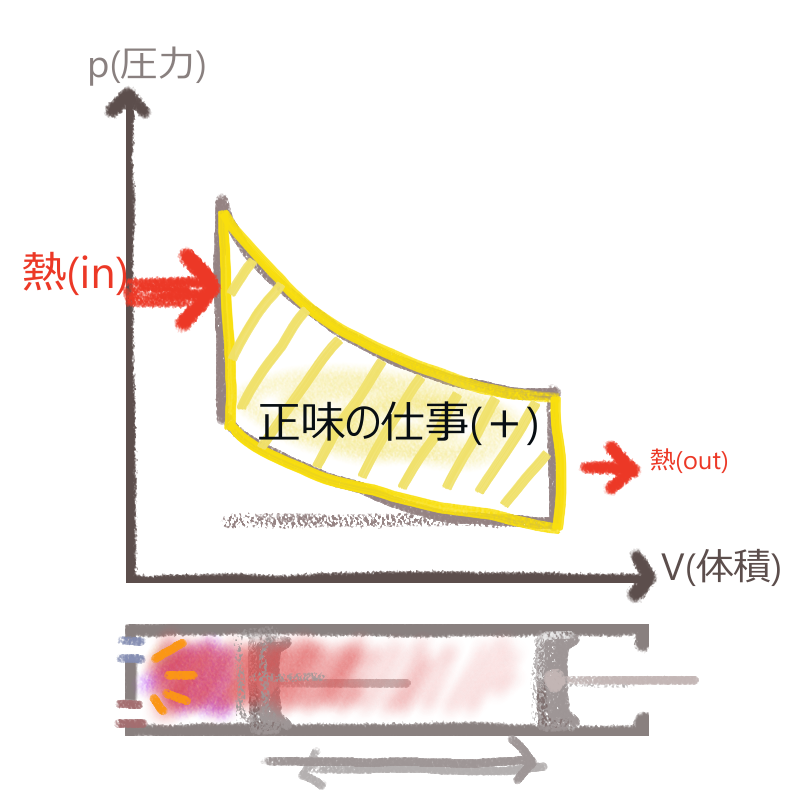
では、得られた仕事量(out)から要された仕事量(in)を引いてみます。
すると、この１サイクルで得られた正味の仕事量が、左図グラフ上の黄色面積部分で表すことができます。
そして、この余剰の仕事量は、手品のようにぱっと現れたわけではありません。③燃焼によって与えられた熱量(in)のおかげです。
それに、④排気のタイミングでシリンダー内に残っていた熱が外部へ出ていっていましたね。これを熱量(out)とし、熱量(in)－熱量(out)の差分をとると、先ほどの正味の仕事量(in－out)を実現するために必要とされた熱量(in－out)がわかります。
つまり、外部から与えられた熱量(in－out)を用いて、外部に与える仕事(in－out)が行なわれた、と考えます。この、熱エネルギーから運動エネルギーを取り出す働きが、エンジン＝熱機関サイクルの基本的な機能となります。
熱効率について
なお、この与えられた熱量(in)を用いて、どれほどの仕事量(out－in)を為すことができたのかを考えれば、そのガソリンエンジンの熱効率がわかります。
式にするとこんな感じです：
$η = \frac{正味の仕事量}{燃焼で上昇した熱量(in)}$
$ = \frac{燃焼で上昇した熱量(in)－排気弁から逃げた熱量(out)}{燃焼で上昇した熱量(in)}$
$ = 1 － \frac{排気弁から逃げた熱量(out)}{燃焼で上昇した熱量(in)}$
ηはイータと読み、熱効率を表す記号です（もとは古代ギリシャ語で、いまのhにあたります）。
なお、この式の中にある「燃焼で上昇した熱量(in)－排気弁から逃げた熱量(out)」とは、ピストンを手前側へ押し戻すのに要された熱エネルギ＝運動エネルギーの意味になります。燃焼で生まれた熱の逃げ道は、排気弁から逃げるほかには、ピストンを押して運動エネルギーになって逃げるしかないためです。これが「正味の仕事量」となります。
これを断熱圧縮や断熱膨張と呼びます。
ミステリー小説でいうところの、「秘密の抜け道はこの部屋にはない！」というお約束のようなものです。
自動車などを駆動するエンジンとしては、熱にはこのピストン押し逃げルートを積極的に使ってもらいたいのが本音です。そのまま車を動かす運動エネルギーになり、有効活用できるためです。排気弁から排気ガスと一緒に出てゆかれても、道路のアスファルト上をますます温めてしまうばかり…。
そんなわけで、エンジンのこの熱効率は、自動車の燃費を左右する主要な要因になっています。
熱効率の改善とガソリン代について
ちなみに、熱効率のさきほどの式は
いろんな過程を踏み、次のようにも表現できます：
$η = 1 – \left\{\frac{1}{圧縮比}\right\}^{気体の比熱比-1}$
「圧縮比」とはシリンダーの$\frac{上死点時MAX体積}{下死点時MIN体積}$のことで、たとえばピストン手前側位置時に1000ccのシリンダー体積が、ピストン押下時に100ccまで縮小する場合、$\frac{1000}{100}$ = 10です。
「比熱比」とは、シリンダー内で点火プラグにより着火される燃料-空気混合気体において、その気体を一定温度だけ上昇させるのに必要な熱量です。ガソリン-空気混合気体の場合、この比熱比は約1.33になるそうです。
これらの値で計算してみると…
$η = 1 – \left\{\frac{1}{10}\right\}^{1.33-1}$
$ = 1 – 0.1^{0.33}$
$ ≒ 0.53$
となり、このガソリンエンジンの熱効率は53%だとわかります。
燃焼により生じた熱のうち、この53%がピストンやタイヤを動かす力になり、残り47%はそのまま排気弁から出てしまったそうです。
この熱効率を、もうちょっと改善してみましょう。
比熱比は気体の性質ゆえ、これ以上どうこうできそうにありません。
そこで、シリンダーのサイズを1000cc→1300ccへと大きくすることで
圧縮比のほうを変えてみます。MIN体積は100ccのままとして、これで圧縮比が$\frac{1300}{100}$=13になったので、こちらで再計算してみると…
$η = 1 – \left\{\frac{1}{13}\right\}^{1.33-1}$
$ ≒ 1 – 0.077^{0.33}$
$ ≒ 0.57$
というわけで、53%→57%へと熱効率が改善しました。
仮に、自動車の燃費＝熱効率と考えて、熱効率53%の車で1年間に2000km走るのに12,000円のガソリン代がそれまでかかっていたとすると、この熱効率4%の改善により、12,000円x$\frac{0.53}{0.57}$≒11,160円となり、約800円ほどお得になります（計算まちがってるかも）。
ただし、実際のガソリンエンジンの熱効率は、機械部品内での摩擦や熱漏れなどが挟まるため、25～30%ほどに留まるそうです。
ともあれ、ガソリンエンジンの熱効率を改善するには、圧縮比がひとつの重要指標であることが以上の計算でわかった（つもりになった）のでした。
さらに知りたいなら…
（←画像クリックでAmazonサイトへ）
各種理論サイクル全般を説明する本です。
エンジンの基本をしっかり学びたい方はぜひご覧ください。本の目次はこちらのサイトをご覧ください。
つまり…
オットーサイクルとは
ガソリンエンジン内で循環する温度・圧力・体積などの諸要素が定式化され、このグラフに基づきエンジン性能の確認や改善などが図られる
という技術原理です。
グラフと聞くと読み解くのが大変なイメージじゃが、それらの数値が、現に激しく動き回るエンジンの荒々しさを表現しているんだと考えると……なんだか胸熱じゃな！
歴史のツボっぽくいうと…
1877年 ドイツのニコラウス・オットーが
４ストロークサイクル（オットーサイクル）の特許を取得。
<参考文献>（2018/09/01 visited）
https://www.sit.ac.jp/user/konishi/JPN/Lecture/Engine/Engine_2ndAll.pdf
